As progressões aritmética e geométrica, estão presentes em nossos cálculos do dia-a-dia de trabalho ou simplesmente quando você está investindo o seu dinheiro numa poupança.

Quando dizemos que iremos distribuir R$ 2.000,00 de abono à 300 empregados e desejamos saber o quanto custará quando a distribuição chegar no 198º empregado, estamos tratando de uma progressão aritmética, isto é, de R$ 2000,00 em R$ 2000,00, adicionadas uma sobre outra, teremos o valor quando chega ao 198º empregado.

Por outro lado, quando dizemos que o saldo da poupança em 31/10/97 era de R$ 2000,00, e em 30/11/97 o saldo subiu para R$ 2400,00, houve uma correção de 20%. Mantendo-se o mesmo percentual, o saldo da poupança em 31/12/97 será de R$ 2880,00. Então dizemos, que houve uma progressão geométrica, cuja a razão foi de 20% ou 1.20.

Resumidamente, uma progressão aritmética elevam-se segundo uma razão, somadas a cada um dos seus termos. Já a progressão geométrica elevam-se segundo, um multiplicador acumulativo constante.

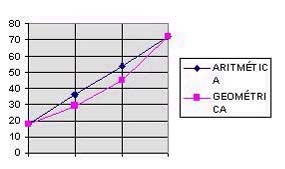
Graficamente, temos:

Note-se que uma progressão aritmética, a sua progressão é sempre linear, isto é, obtém-se uma linha reta. Já a progressão geométrica, a sua progressão é sempre uma curva.

Assim, quando quisermos determinar uma faixa salarial, através de uma progressão, tendo em vista o número de faixas à serem distribuídas, o menor e o maior salário, podemos resolver da seguinte forma, através de exemplos:

a) Determinação através da Progressão Aritmética:

fórmula: q = (an - am) : (n - 1)

Exemplo:

Desejamos distribuir os salários de R$ 800,00 a 1800,00 em 11 faixas, através da progressão aritmética. Temos então:

q = (1800,00 - 800,00) : (11 - 1)

q = 1000,00 : 10

q = R$ 100,00

Portanto, a distribuição de faixas será a seguinte:

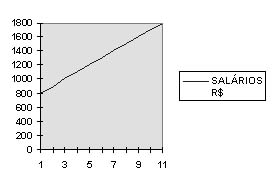
Note-se que as faixas sobem em R$ 100,00 para cada faixa. Esta progressão tem a razão de R$ 100,00.

Gráfico:

b) Determinação através de Progressão Geométrica:

Utilizando o mesmo exemplo, apliquemos a seguinte fórmula da razão da Progressão Geométrica:

fórmula:

q = ^n-1Ö (an - am)

Temos portanto:

q = ^10Ö (1800,00 : 800,00)

q = ^10Ö 2,25 à ou seja 2,25^{(1 : 10)}

q = 1.084471771

Portanto, a distribuição de faixas será:

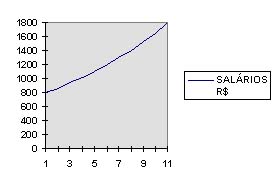
Note-se que as faixas crescem a razão de 1.084471771

Gráfico:

Cálculos de amplitude das faixas salariais:

A amplitude deve ser entendida como a distância que tem entre a menor e a maior faixa salarial. Exemplo: Quando dizemos que o menor salário é R$ 800,00 e maior é R$ 1200,00, numa determinada faixa salarial, a amplitude é de:

(1200,00 : 800,00) = 1.5 ou 50%

Portanto, de R$ 800,00 até R$ 1200,00, tem 50% de amplitude.

Questões:

a) Temos o menor salário de R$ 890,00 e o maior salário de R$ 1635,00, distribuídas em 5 faixas salariais, queremos que calcule o salário mínimo, médio e máximo de cada uma das faixas, com a amplitude de 25%.

Solução:

q = ^{5 -1Ö} (1635,00 : 890,00)

q = ^4Ö 1,837078652 à ou seja 1,837078652^(1/4)

q = 1.164211641

A distribuição das faixas ficará assim:

Vamos assumir que os respectivos salários, estejam na faixa média. Devemos, portanto, achar a faixa mínima e a faixa máxima, de maneira que a amplitude seja 25% ou 1.25.

Fórmula:

amplitude = Ö 1.25 = 1.118033989

Dividindo os salários das respectivas faixas pelo índice da amplitude, temos como resultado a "faixa mínima" e multiplicando, temos a "faixa máxima".

Vejamos na página seguinte como ficarão:

O cálculo do salário mínimo da faixa A, foi elaborado da seguinte maneira:

R$ 890,00 : 1.118033989 = R$ 796,04.

Para o cálculo do salário máximo:

R$ 890,00 x 1.118033989 = R$ 995,05,

e assim sucessivamente.

b) Seguindo a tabulação e cálculo anterior, desejamos elaborar uma tabela de faixas salariais com os mínimos, médios e máximos, levando-se em consideração que o menor salário da faixa seguinte, seja o médio da faixa anterior. E o maior salário da anterior, seja o médio da faixa seguinte, e assim sucessivamente.

Vejamos como fica isso graficamente:

Solução:

1º passo: toma-se o salário médio e divide-se pela razão da PG, no nosso exemplo é de 1.164211641, você encontrará o salário mínimo da faixa;

2º passo: tomando-se o mesmo índice e multiplicando pelo salário médio, você encontrará o salário máximo da faixa.

Portanto:

salário mínimo = R$ 890,00 : 1.164211641 = R$ 764,46

salário máximo = R$ 890,00 x 1.164211641 = R$ 1036,15

E assim sucessivamente ...

Vejamos a seguir, como ficarão:

c) Seguindo a tabulação e cálculo inicial, desejamos elaborar uma tabela de faixas salariais com os mínimos, médios e máximos, levando-se em consideração que o maior salário da faixa anterior, seja a menor da faixa seguinte e assim sucessivamente.

Vejamos como fica isso graficamente:

Solução:

1º passo: toma-se o índice da PG e acha a raiz quadrada (Ö );

2º passo: tomando-se como base o valor do salário médio e dividindo-se pelo índice do 1º passo, você encontrará o salário mínimo e multiplicando, encontrará o salário máximo.

Portanto:

Ö 1.164211641 = 1.078986395

salário mínimo = R$ 890,00 : 1.078986395 = 824,85

salário máximo = R$ 890,00 x 1.078986395 = 960,80

E assim sucessivamente ...

Vejamos os resultados: