Recursos Humanos
Ferramentas de RH
Matemática e Estatística Aplicada a Administração de Pessoal/RH
Noções de Correlação
O estudo dos problemas em que intervêm duas variáveis é interessante para o administrador de empresa, não apenas porque uma quantidade pode ser prognosticada a partir dos valores de outra, como também pela relação mútua que pode existir entre as medições.
Os primeiros problemas de correlação estão associadas ao nome de GALTON em razão de seu estudo sobre características herdadas, isto durante a segunda metade do século passado.
Seus estudos despertaram o interesse de muitos matemáticos e biólogos que concorreram entre si para o desenvolvimento da teoria e suas aplicações.
O resultado disso abarcou um grupo de conceitos desenvolvidos sob o nome de REGRESSÃO, de forma que, na literatura estatística, dificilmente se distinguia uma de outra matéria.
Uma das consequências do estudo da correlação, é o estabelecimento de uma medida da aproximação do ajuste, mas em sentido relativo.
Assim, se a um conjunto de valores "x" e "Y" tivermos ajustado uma linha reta, pelo emprego do método de mínimos quadrados, podemos medir o grau de precisão do ajustamento, até o ponto em que o ajustamento pela função (equação) escolhida foi bom.
Estaremos expressando por um número a qualidade do ajustamento. Podemos dizer, então, que o estudo visando ao ajustamento de uma linha reta pode ser completado pelo emprego da análise da correlação, de forma a se poder medir até que ponto o ajustamento foi bom ou não.
Vamos supor que, através de um ajustamento pelo método de mínimos quadrados, tenhamos chegado a seguinte função linear (equação de linha reta):
Y = a + bx |
Quando isto ocorre, dizemos que existe correlação (neste caso, correlação linear) entre X e Y, ou então, que Y está correlacionado a X, ou ainda, menos rigorosamente, existe uma dependência linear de Y a X.
Resta saber se esta dependência é forte ou fraca, o que será feito através do coeficiente de correlação, que possibilita a consecução de uma medida da aproximação do ajustamento.
As vezes ocorrer uma relação recíproca (mútua) entre duas variáveis ou atributos, a qual pode ser expressa por uma linha reta.
O coeficiente de correlação possibilita, mesmo nesse caso, estabelecer até que ponto a linha reta pode ser representativa d relação entre essas variáveis.
Seria o caso, por exemplo, de analisarmos as notas obtidas pelos alunos de uma mesma classe em duas matérias afins, Matemática e Estatística, para verificar se estas notas estão correlacionadas, ou seja, se existe uma relação linear entre elas.
A relação entre essas notas, se houver, é mútua, não sendo possível distinguir a variável independente da dependente.
O coeficiente de correlação linear calculado a partir de uma amostra de "N" pares de valores de duas variáveis é simbolizado universalmente pela letra "r".
Este coeficiente só deve ser interpretado em sentido relativo (em termos percentuais) e mede até que ponto o ajustamento de uma linha reta é bom ou não.
Trata-se de um número que pode tomar qualquer valor entre + 1 e - 1. Seu sinal é o mesmo que o de "B", coeficiente angular no ajustamento de uma linha reta e indica se a correlação é positiva ou negativa, enquanto que o valor absoluto de "r" indica o grau de associação (relação) existente entre as variáveis estudadas.
Vejamos agora, com a existência ou não da correlação linear pode ser observada através de um diagrama de dispersão.
Em primeiro lugar, exemplificaremos os dois casos extremos, aqueles em que o coeficiente de correlação assume os valores + 1 e - 1.
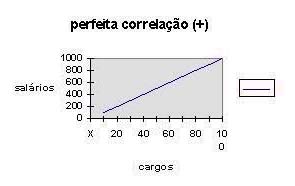
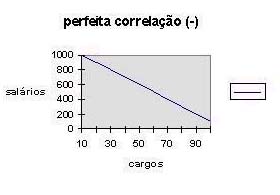
Quando um desses casos ocorre, conforme pode ser observado nos gráficos A e B, dizemos que as variáveis estão perfeitamente correlacionadas, ou que há correlação perfeita entre elas.
Estes dois casos são, porém, difíceis de serem encontrados na vida real, sendo mais comuns em casos intermediários, como aqueles em que o coeficiente de correlação é maior do que -1 ou menor do que +1.
|
|
No gráfico esquerdo temos uma correlação linear perfeitamente positiva. Há uma correlação porque as variáveis X e Y estão relacionadas, estão associadas mediante uma relação funcional (equação).
Essa correlação é linear, pois a relação funcional, a equação, que estabelece simbolicamente a associação entre X e Y é de uma linha reta.
Além disso, a correlação linear é perfeita porque todos os pontos estão perfeitamente alinhados, quer dizer, todos estão situados exatamente sobre a linha reta.
Por último, a correção é positiva porque o sinal de B, coeficiente angular da reta ajustada, é positiva, o que equivale a dizer que as variáveis crescem no mesmo sentido: quando os valores de X crescem, os de Y também crescem; quando os valores de X decrescem, os de Y decrescem igualmente.
No gráfico direito acontece situação semelhante. A única diferença é que neste caso é negativo.
Fica configurado, então o caso de correlação linear perfeita negativa.
O significado do sinal negativo é de que quando os valores de X crescem, os valores de Y decrescem; quando os valores de X decrescem, os valores de Y crescem.
Como dissemos anteriormente, estes casos são extremos. Configurações intermediárias de diagramas de dispersão são mais corriqueiras.
Vejamos mais alguns exemplos de digrama de dispersão, que representem outros valores de "r" que não +1 ou -1.
Podemos agora ver como se determina o coeficiente de correlação para termos uma avaliação quantitativa do grau de ajustamento da linha reta aos pontos do diagrama de dispersão.
A fórmula que nos permite determinar o valor do coeficiente de correlação linear é a seguinte:
r = [N å XY - (å X) (å Y)] : Ö [N å X2 - (å X)2] [N å Y2 - (å Y)2] |
X |
Y |
XY |
X2 |
Y2 |
1 |
5 |
5 |
1 |
25 |
2 |
10 |
20 |
4 |
100 |
3 |
12 |
36 |
9 |
144 |
4 |
20 |
80 |
16 |
400 |
å = 10 |
47 |
141 |
30 |
669 |
r = [N å XY - (å X) (å Y)] : Ö [N å X2 - (å X)2] [N å Y2 - (å Y)2]
r = [4 x 141 - (10) (47)] : Ö [4 x 30 - (102)] [4 x 669 - (472]
r = (564 - 470) : Ö (120 - 100) (2676 - 2209)
r = 94 : Ö (20 x 467)
r = 94 : 96.64367543
r = 0,972645127 ou seja 97,26%
O valor de "r" é quase próximo de 1.0, donde se pode concluir que o ajustamento da linha reta aos pontos marcados no diagrama de dispersão é quase perfeito.
Trata-se portanto, de um bom ajustamento. Como "r" é positivo, podemos dizer que as variáveis "x" (pontos de cargos) e Y (salários) variam no mesmo sentido, isto é, quando aumentamos os pontos dos cargos, os salários também aumentam.